차가 없던 시대 혹은 대다수가 차를 이용하지 않았던 시절에는 순간순간의 속력을 알기도 어려웠고 구태여 알려고 하지 않았다. 두 장소 사이의 거리 그리고 그 거리를 걸어가는데 걸리는 시간이 일상에서 중요했다. 물리학의 관점에서 이야기한다면, 이동거리와 평균 속력의 개념이다. 평균 속력은 어느 정도의 거리를 가는데 어느 정도의 시간이 걸렸는지를 따지는 것이다. 물론 속력은 빠르기, 즉 같은 거리를 가더라도 얼마나 시간이 적게 걸리느냐에 따라서 더 빠른 것이다. 수식으로 표현하자면 평균 속력은 이동한 거리를 걸린 시간으로 나눈 것이다. 시간이 분모에 있기 때문에, 분자인 이동거리가 같다고 하더라도 분모인 시간이 작을수록 속력은 빨라진다. 마찬가지로 같은 시간이라고 하더라도 더 많은 거리를 이동하였다면, 분모가 같아도 분자가 커져서 속력이 빠르다. 여기서 속력과 평균속력을 섞어서 사용했는데, 그렇게 이야기해도 혼동되지 않기 때문이다. 그러나 직접 자동차를 운전하면서 계기판을 바라보거나 내비게이션에 나타난 속도를 본다면 혹은 과속 단속 카메라에 접근하면서 내비게이션에서 알려주는 안내 음을 들으면, 두 장소 사이를 주파하는 속력이 아니라 그 순간의 속력이 중요하다는 것을 깨닫는다. 단속 카메라를 지날 때 차의 속력을 제한속도보다 낮추어야겠다고 생각할 것이다. 이때의 속력은 순간 속력에 해당한다.
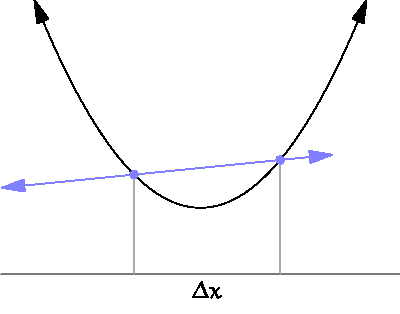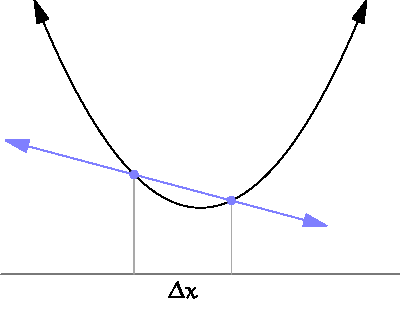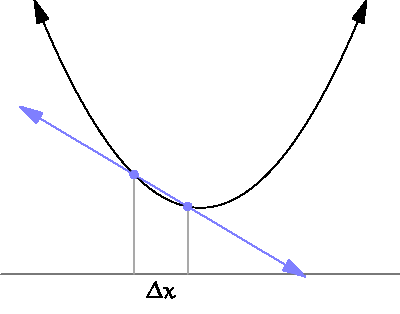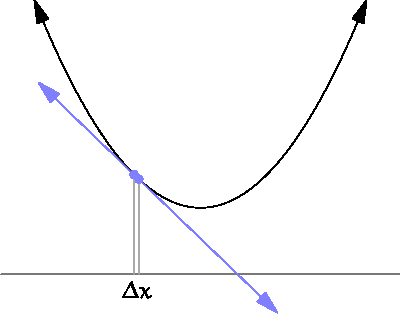
그러면 순간 속력은 평균 속력과 무엇이 다를까? 어떻게 구별할 수 있나? 물론 일상에서 우리는 경험을 통하여 순간마다 속력이 달라지는 순간 속력의 세상에 살고 있으며, 그러한 순간 속력들의 평균을 평균 속력이라고 생각할 수 있다. 그리고 경험으로 구별하는 것처럼 물리적으로도 더 엄밀하게 구별할 수 있다. 언어적으로는 그 순간의 빠르기라고 순간 속력을 말할 수 있지만, 수학적 혹은 물리적으로는 아주 짧은 시간 동안 이동한 거리를 말한다. 이렇게 아주 짧은 변화에 대하여 무엇이 변하는 것을, 수학적으로 미분(微分 differentiation)이라고 한다. 한자의 뜻처럼 아주 작은 것으로 나눈다는 의미다. 즉, 평균 속력은 유한한 시간 동안에 움직인 거리라고 할 수 있고, 순간 속력은 순간 혹은 아주 짧은 시간 간격동안 움직인 거리로 표현할 수 있는 것이다. 어찌 보면 둘 사이의 차이가 그렇게 중요하게 생각되지 않을 수도 있지만, 미분은 변화를 기술하는 유일한 수학적 도구로써 무엇이든지 변하는 것에 대해서 미분이라는 발명품을 사용하여 정확한 계산과 예측을 할 수 있게 된다.
차에 익숙하지 않던 시절에 가졌던 시간과 거리 그리고 속력이라는 관념이 현대에서는 속력을 평균 속력과 순간 속력으로 구분하게 만들었고, 순간 속력에 대한 감각과 경험에 낯설지 않은 세상에서 우리는 살아간다. 조금 더 나가보자. 현대인이 순간 속력을 고려하는 것은 속력이 순간마다 변하는 것이기 때문이다. 만약에 순간 속력이 변하지 않는다면, 순간 속력과 평균 속력은 아무런 차이가 없다. 변하지 않는 순간 속력을 평균하여봤자 평균 속력과 순간 속력은 구별할 필요가 없이 같다. 이렇듯 속력이 순간마다 변하는 경우에나 순간 속력의 의미가 살아나고, 속력이 순간마다 변한다는 것의 의미가 새롭게 등장한다. 즉 얼마나 빨리 속력이 변하는가. 가령 정지 상태에서 시속 100 km가 되는데 걸리는 시간으로 차의 성능을 평가하는 지표가 되곤 한다. 흔히 제로백(0-100)이라고 불리기도 하는 이 지표는 차의 초기 가속 성능을 평가하는데 사용되는데, 정상급의 빠른 차들은 채 3초가 걸리지 않는다고 한다. 여기서 가속이라는 말이 등장하는데, 가속은 가속도(acceleration)을 줄인 말이며, 속력이 증가하든 감소하든지 간에 속력의 변화를 나타내는 용어다. 가속도는 대부분의 세상을 거의 완벽하게 기술하는 고전역학의 가장 핵심적인 개념이며, 바로 뉴턴의 운동 제2법칙인 F = m a “힘은 질량과 가속도의 곱이다”에 등장하며, 운동을 결정하는 물리량이다. 이 짧은 글에서는 차를 타고 가볍게 거리에서 평균 속력을 지나 순간 속력에 이르렀다가 가속도에 이르렀다. 짧은 글치고는 분에 넘치게 중요한 개념을 말하면서 생략된 것이 많지만, 이전에 사용하던 상식적으로 사용하던 내용들에서 조금 더 나아가 수 있다면 아쉬움은 크지 않을 것 같다.
이미지 출처 : http://asq.kr/bJ7PXc4C0FhWM http://asq.kr/LzTLloISe4u8R