현실에서 파동 하나만 존재하는 경우도 있지만, 파동들이 서로 만나는 경우를 흔하게 볼 수 있다. 가령, 호수에 두 개의 돌을 던지면 각기 다른 두 개의 파가 전달되면서 호수표면의 모든 점들에서 두 개의 파동이 만나며, 일상에서 우리들 귀로 다양한 소리들이 섞여서 들어온다. 이렇게 두 개 이상의 파동이 만나는 것을 파동의 중첩(superposition)이라고 한다.
파동방정식을 통하여 중첩을 이해하도록 하자. 여기서 파동방정식을 풀거나 하는 수식적인 것을 알지 못해도 상관없다. 단지, 이렇게 이미 정리된 것이니 여러분들은 그 과정을 직접 풀어내지 못하고 받아들여도 괜찮으며, 수식보다는 물리적 이해를 하는 것이 더 중요할 수도 있다.



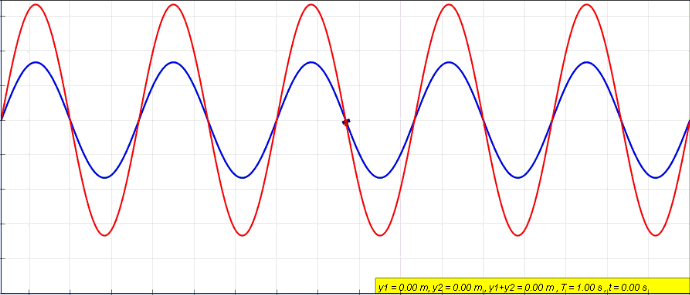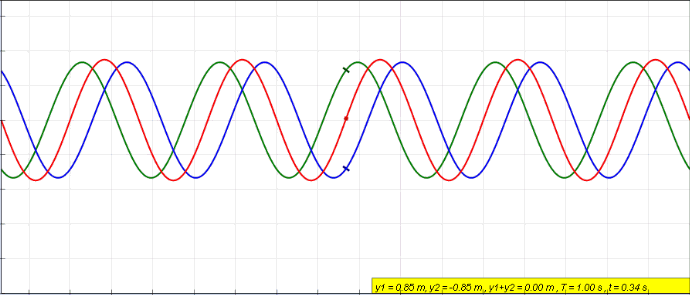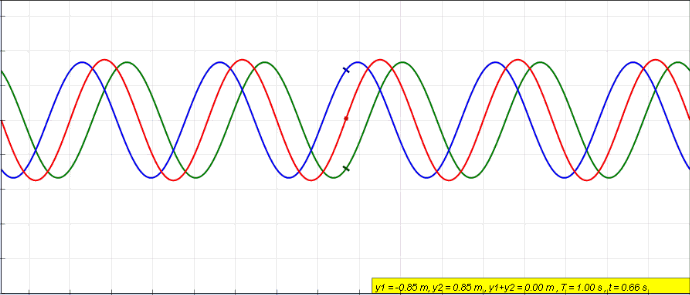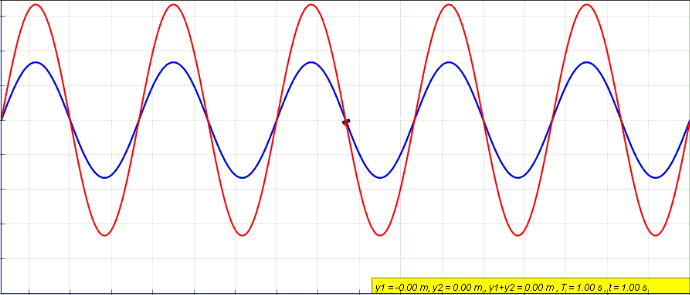
각 파동의 변위는 삼각함수로 표시되고 파동들의 합은 다시 삼각함수로 표현되지만, 진폭에 변화가 생긴다. 똑같은 사인파가 두 곳에서 발생한 경우를 생각해보자. 두 파동의 해를 각각 r_1 (x, t)=A sin(kx-ωt), r_2 (x, t)=A sin(kx-ωt+ φ)로 표시하면, 같은 파동방정식을 만족하는 해인 r_1 (x, t)+ r_2 (x, t)= r(x, t)는 삼각함수의 덧셈공식을 이용하여 다음과 같이 표현할 수 있다.
r(x, t)=2A cos(φ/2) sin(kx-ωt+ φ/2) (식 ⑥)
여기서 φ는 두 파동의 위상차이며, 중첩된 파동의 진폭이 위상에 따라 달라지는 것에 주목하자.
위상차 φ는 위치에 따라 달라지는 값이기 때문에, 합성된 파동의 진폭 2A cos(φ/2)이 위상차에 따라 달라진다. 즉, 매질은 어느 위치에서는 진폭이 2A로 증가하여 진동하고, 어느 위치에서는 정지해 있다. 코사인 함수는 ±1/2π, ±3/2π, ±5/2π, … 일 때, 0이 됨을 알고 있다. 위상차 φ가 π의 홀수배 위치에 있는 매질은 진동하지 않고 정지해 있는 것이다. 이렇게 소멸된 중첩을 상쇄간섭이라고 한다. 반대로 위상차가 π의 짝수배 위치에 있는 매질은 진폭이 2A로 진동하며 이렇게 증폭된 중첩을 보강간섭이라고 한다. 삼각함수의 덧셈공식은 e^iθ=cosθ+i sinθ 를 이용하여, e^iα e^iβ=e^(i(α+β)) 양변의 실수부와 허수부를 비교하면 외울 필요 없이 간단하게 얻을 수 있다.
어느 지점에서 매질의 변위를 해로 갖는 파동방정식은 선형 방정식이므로, 각각의 파동방정식의 해들을 합하여 중첩된 파동의 해를 구할 수 있다. 각각의 파동방정식의 해는 삼각함수로 표현되고 중첩된 파동의 해는 삼각함수의 덧셈정리를 이용하면, 또 다른 삼각함수로 표현되는 파동형식의 수학적 해를 구할 수 있다. 두 파동이 얼마나 결 맞게(수학적 표현으로는 두 파동이 만날 때의 위상차에 따라)만나느냐에 따라 파동의 형상, 파형이 달라진다. 수학적인 관점에서 중첩은 이렇게 말끔하게 기술할 수 있는데, 물리적으로는 어떻게 설명하는 것이 좋을까?
한 파동에 의하여 단위물질(분자나 원자)이 흔들리며 진동하고 있는데, 다른 파동에 의하여 다른 진동이 진동하고 있는 단위물질에 진동을 전한다. 떨어져 있던 두 입자(혹은 물체)의 상대적 운동에 의해 한 점에서 만나는 것을 충돌(collision)이라고 부르는데, 질점의 경우는 운동량이 보존되는 탄성 충돌(elastic collision)이 된다.[1] 두 단위물질의 진동이 만나는 것을, 진동하고 있는 두 질점의 탄성충돌로 볼 수 있을 것이다. 한 질점의 운동과 같은 방향으로 운동이 전해진다면 그 질점의 운동은 증폭되고, 서로 운동방향이 다를 때 두 질점의 진동이 만난다면 운동은 감쇄할 것이다. 이렇게 파동의 중첩에 대해서도 우리는 (질점, 입자로 볼 수 있는) 미시적 단위물질의 진동모형으로 이해할 수 있다.

그런데 뭔가 이상하다. 중첩은 파동의 성질이 아닌가? 파동의 간섭(interference)은 두 파동의 중첩되며 위상차에 따라서 보강(위상이 같을 때)되거나 소멸(위상이 반대일 때)되는 현상이다. 즉, 간섭무늬는 무엇이 입자가 아니라 파동이기 때문에 나타나는 파동의 대표적 특징이라고 우리는 알고 있다. 어떻게 된 일일까? 입자로 설명하지 못한다고 하는 파동의 또 다른 대표적인 성질인 회절(diffraction)도 살펴보자.
[1] 내부적인 구조를 갖고 있는 물체의 경우에 비탄성 충돌에서 역학적 에너지가 보존되지 않지만, 내부에너지와 열을 증가시키면서 계의 전체 에너지는 보존된다.